해당 글은 APPLIED SCIENCES-BASEL의 9권 20호에 게재된 'Deep LSTM with Reinforcement Learning Layer for Financial Trend Prediction in FX High Frequency Trading Systems'을 리뷰하는 포스팅입니다. 첨가하거나 수정할 부분이 있을 수 있습니다. 해당 부분에 대해선 공부하면서 서 수정을 진행하겠습니다.
Abstrct
High-frequency trading(HTF)은 주식, 선물, 채권 시장에서 수학적 알고리즘을 사용하여 고빈도의 거래를 하기위해 정교한 소프트웨어 툴과 혹은 하드웨어를 포함하는 금융시장에 개입하는 방법중 하나이다. 고빈도 전략은 주식 거래의 70%를 초과할 정도로 측정되고 있다. 고빈도 트레이딩 시스템에서의 주된 이슈중 하나는 중단기 트랜드의 예측이다. 이러한 이유로 이러한 주제로 많은 논문들이 제출되었다. 저자는 이 논문에서 딥러닝과 강화학습을 사용하여 환율시장에서의 고빈도 트레이딩 이익을 극대화 하는 방안을 제안한다. 제안된 알고리즘은 과거 트랜드와 다른 연관된 환율 정보를 통해 차액거래 기법을 사용하여 85%정도의 정확도로 중단기 환율 트랜드를 예측할 수 있다. 제안된 파이프라인의 마지막 부분에서 *grid trading engine을 사용하여 이득을 최대화 하고 구매량을 최소화한다. 이 트레이딩 시스탬은 EUR/USD 환율에서 지속성있는 투자자본 수익율(98.23%)과 구매량 감소(15.97%)이 여러해에 걸쳐 검증되었다.
*Grid Trading : 손실을 줄이기 위해 기준 가격에서 특정 단위를 정해 해당 단위 윗가격와 아랫가격에 순차적으로 매도와 매수를 거는 것을 말한다. 트랜드에 따라 어떻게 거는지가 달리진다.
1. Introduction
시장의 트랜드를 아는 중요한 포인트는 중기와 장기 트랜드 모두를 올바르게 추정하는 것이다. 시계열 금융 데이터를 보면 많은 트랜드가 반복되는 그래프 패턴을 통해 알 수 있는 잘 확립된 움직임을 따른다는 것을 볼 수 있다. 그러나 트래이딩 시스템에서 현재의 트랜드를 밝히는 것뿐 아니라 나아가 시장의 트랜드를 바꾸는 첫번째로 잠재된 시그널을 밝히는 것에 관심이 있다. 일반적으로 짧은 과도기적 구간이 금융 시장의 트랜드가 바뀌기전 선행된다. 확실히 이러한 사실이 주식과 채권시장에 그렇다면, 환율시장에서는 주식시장보다 훨씬 많은 량의 거래가 일어나므로 잘 적용된다. 많은 트래이딩 알고리즘은 현재의 트랜드와 변화를 알리는 시그널을 분석된 금융 산업과 연관된 다른 것들에 관한 관련된 연구를 통해 찾으려 한다. 그 중 많은 트레이더들이 연관성을 통해 찾으려고 하는 방법중 하나는 흔히 차액거래라고 불리는 것과 관련되어 있다. 금융시장에서 차액거래는 같은 시간에 아직 관련된 다른 환율 정보가 적용되지 않아 가격의 차이가 있을 때 일어날 수 있다. 이러한 방법은 많은 환율이 관련된 다른 환율에 영향을 받기 때문에 더 투자할 만한 가치가 있다. Figure 1은 이러한 예시를 보여준다.

우리는 위에서 말한 것에서 환율 시장은 거시경제요인, 국가와 국제적 통화 정책 그리고 군사 분쟁등과 같은 영향을 받는 비선형적, 유동적인 것을 포함한다는 점을 더할 것이다. 이러한 사실들은 트래이딩 시스템이 신중한 손실방지책을 기반으로 적절한 금융 보사액과 손실 방지책을 제공하더라도 장기적으로 불확실성을 예측불가능성을 만들고 단기적으로는 더 큰 영향을 가진다. 이러한 이유로 저자는 짧은 시간 동안 연속된 거래에서의 이득을 통해 틀린 거래를 통한 손실을 보완하는 방법을 제안한다. 이러한 점은 또한 중단기 트랜드의 분석을 기반으로 신중한 트래이딩 전략을 사용하는 많은거래를 통해 보완할 수 있다. 저자는 LSTM(long short-term memory)와 같은 지도학습을 기반으로 딥러닝 방법을 통한 주식시장과 통화 시장에서의 고빈도 트래이딩(HTF) 알고리즘의 개발을 조사했다. 결과는 제안된 알고리즘의 정확도와 환율시장에 적용한 grid strategy때문에 만족스러웠다.
많은 논문에서 저자들이 효율적 트래이딩 시스탬 구축을 위해 딥러닝과 강화학습 방법을 사용했다. 아래의 글은 딥러닝과 강화학습을 통해 알고리즘을 고안하는 과학적 논문들이다.
1.1 Deep Learning(LSTM) and RL Based Trading Systems : Literature Review
[6]
저자는 딥강화학습을 사용하여 흥미로운 트레이딩 접근을 제안하였다. 저자는 딥강화학습을 통해 수정된 deep Q-network(DQN)과 actor-critic(A3C) 접근 방법을 사용하여 자동으로 매매하는 거래 agent를 제안하였다. 그들은 실제 거래 환경에 맞는 알고리즘을 위해 stacked denoising autoencoder(SDAEs)와 LSTM을 사용하여 deep framework를 구현하였다. 결과는 제안된 방법의 효율성을 보여주었다.
[7]
하루동안의 multi-objective 트레이딩 방법을 제안했다. 가장 중요한 아이디어는 하루 내 금융 시그널과 거래를 위한 multi-objective 딥 강화학습방법이다. 저자는 연속된 거래 결정을 하는 강화 학습 프레임워크 (ad-hoc LSTMs과 함께)의 앞에 사용할 시장의 깊은 특징을 얻는 심층신경망 모델을 구현하였다. 이익과 손해의 적절한 균형을 위해 저자는 각각의 가중치를 가진 이익과 손해를 위한 두개의 목적 function을 포함하는 multi-objective 최적화 방식을 제안했다. 사용량에 대한 분석은 없었지만 실험적 결과는 제안한 방법이 효과적인 것을 보여주었다.
[8]
저자는 에너지 트래이딩의 개념을 사용한 획기적 방법을 고안하였다. 제안된 전체적 마켓 모델에서 prosumer 의 에너지 트레이딩 ad-hoc 수학적 전략을 통해 prosumer의 의사결정 방식을 Markov decision process를 통해 분석함으로써 일부 시장 참여를 experience replay 방식을 사용한 심층 강화 학습 방식을 통해 규명하였다. 이 방식은 에너지 관리 분야의 회사 주식 참조를 통해 금융시장에 쉽게 확장할 수 있다. *quantitative finance에서 가장 잘 연구된 지표는 금융 변동성이다. 휴리스틱하게 특정 금융 상품의 변동성을 계산하는 많은 방법이 있다. 많은 트레이딩 시스탬이 금융 상품의 변동성을 기반으로 하기때문에 효과적인 변동성 예측 모델을 가지는 것은 중요하다.
*quantitative finance : 수학적 모델과 엄청나게 많은 데이터를 사용하여 금융 시장을 분석하는 방법
[9]
저자는 루피와 달러의 환율 변동성 예측 파이프라인을 제안하였다. 최근 심층 LSTM 아키텍쳐를 통해 루피와 미화의 변동성은 성공적으로 분석되었다. 해당 연구는 일간 변동성에서 상승세와 하락세를 예측하는 혁신적인 방법을 제안하였다. 저자는 LSTM모델과 회귀 신경망, SVM, random forest, 회귀 아라고리즘, 결정 트리와 boosting technique을 비교하였다. 가장 효과적인 모델은 LSTM으로 드러났다.
[10]
저자는 Shanghai Composite Index. 거래에 적용해 딥러닝 기반의 다양한 모델들을 분석했다. 조사 결과는 딥러닝 기반의 거래 전략 중 적은 변동성을 가진 시장에서 높은 정화가도를 가진 모델이며, 이는 투자자가 만족스러운 이익을 얻으며 리스크를 줄일 수 있기 때문이미을 밝혀냈다.
[11]
저자는 수익율이 좋은 거래 시스템을 위해 금융 기록에 저장된 거래 전략을 복제하는 매우 흥미로운 전략을 제안하였다. 많은 량의 금융 데이터에서 결정 방법과 주요한 특징을 뽑아 내는 것은 매우 어렵다. 이러한 이유로 저자는 거래 전략을 구사하는 전문가를 흉내내는 강화학습 모델을 제안하였다. 저자는 전문가의 거래 전략을 모방하는 ad-hoc 정책 경사법을 구현하기 위한 강화학습 환경을 디자인했다. 실험 결과는 제안된 강화학습 파이프라인이 training 세션과 validation 세션에서 80% 가량 잘 작동하는 것을 보여주었다.
1.2. Deep Computing-Based Trading Systems: Literature Review
[12]
저자는 multi-agent 기반인 A-trader system으로 불리는 흥미로운 방법을 제안하였다. 저자는 외환시장에서 수익율 좋은 거래 전략 A-trader 프레임워크의 적용법을 분석하였다. 실험결과를 통해 분석된 강화학습 H20 알고리즘이 더 잘작동하는 것 처럼 보였다.
[13]
저자는 1D CNN을 기반으로 제안한 새로운 모델과 함께 다양한 모들들을 분석하고 비교하였다. 제안된 CNN 모델은 다른 금융 데이터를 거래 전략에 사용하는 대신 잠재적 특징들을 얻어내는데 사용하였다. 저자는 2010년 1월부터 2017년 10월까지의 과거의 6개 미래를 통해 full back-testing 을 사용하여 그들의 방법을 검증하였다. 결과는 매우 좋아보였다.
...
아래의 선행연구의 경우 내용이 간략한 내용설명만 있으므로 생략
...
2. Materials and Methods
논문에서 제안하는 방법은 중기 트랜드를 예측하기 위해 다른 통화들의 관계를 이용하는 것이다. 논문의 끝에서 저자는 외환시장에서 차액거래 기회를 특징짓는 외환 거래를 기반으로 하는 파이프라인을 기술한다. 첫번째 섹션에서 소개했던 것 처럼 차액거래는 동일한 시간의 가격 차이를 이용한다. 차액거래의 주된 예시는 삼각 차액 거래이며 이는 세 환율 중 하나의 환율이 다른 두개의 환율로 얻어지는 것을 이용한다. 이 논문에서는 EUR/USD, GBP/USD 그리고 EUR/GBP를 사용한다. 다른 세개의 환율에서도 비슷한 방법이 사용될 수 있다. 거래에 사용할 환율은 EUR/USD이다. 외환시장에서 EUR/USD의 환율은 항상 EUR/GBP와 GBP/UDS의 관계를 통해 얻어 질 수 있다.

식(1)에서 $p_x(t_k)$는 화폐의 가격을 나타낸다. 그러므로 만약 안정된 금융 시장의 경우 즉, 투자자가 차액거래의 이점을 보지 못하고 결과적으로 규칙적인 이익을 얻는다면 식(1)은 항상 옳다. 다시말해, 항상 매우 정확한 환율을 가지고 있다. 실제로는 외환시장에서 짧은 가격의 불일치는 항상 찾을 수 있으며 이는 자동으로 거래를 진행하는 로봇에게 이익을 얻을 훌륭한 기회이다. 저자는 빠르게 가능한 다른 환율 사이의 가격 불일치를 나타내며 시계열 환율 차트에서 찾을 수 있는 특정과 디자인을 조사중이다.
위에서 언급한 이유로 저자는 주어진 통화에서 중기 트랜드를 결정하기 위해 삼각 차액거래 상황에서 관련된 통화의 관계를 분석하는 파이프 라인을 디자인했다. 특별한 케이스에서 일반화를 잃지 않고 저자는 EUR/USD 환율을 거래를 하는 것으로 EUR/GBP와 GBP/USD 환율을 삼각 차액거래가 가능한지 결정하는 요인으로 하겠다. 이는 비슷한 금융 특성을 가진 다른 환율에도 적용 가능하다.
이러한 전제를 가지고 저자는 아래에 파이프라인을 제안한다. Figure 2는 저자가 말하려고 하는 알고리즘의 파이프라인 블럭 다이어그램을 보여준다.

이어지는 문단은 위의 그림에서의 블락을 각각 설명할 것이다.
2.1 Data Pre-Processing Block
이 블럭의 목적은 들어오는 시계열 금융 데이터를 전처리 하는 것이다. 특히 이 블럭에서 시계열 입력값들은 [0, 1]의 구간 내로 일반화 된다. Figure3 은 논문에서 분석된 세개의 환율 정보가 일반화 된 것을 보여준다. 이러한 방식으로 어떠한 환율 정보가 들어와도 파이프라인은 항상 [0, 1] 구간의 데이터만 처리하게 되며 이것은 제안된 알고리즘의 안전성을 향상시킨다.

학습과 검증을 하기위해 저자는 적절한 금융 가격 데이터를 준비했다. 구체적으로 말하면, 99% 정확도로 2004-2018 구간의 EUR/USD, GBP/USD, EUR/GBP의 과거 금융 정보를 모았다. 다시말해 앞서 말했던 구간을 시가와 종가, 고가와 저가 그리고 각 가격의 시간을 모았다. 이 데이터셋을 학습을 위한 데이터와 검증과 시험을 위한 데이터로 나누었다. 구체적으로 말해 한해의 데이터 중 70%는 학습을 위해 30%는 검증을 위해 사용되었다. 딥러닝에서의 overfitting을 피하기 위해 학습 데이터와 검증 데이터 모두 가능한 트랜드(장기, 단기, NULL)가 동일하게 나타나는지 보기위해 검증하였다.
따라서 금융 정보는 전처리 시스템의 입력값으로 사용되며 이는 후에 딥러닝 블럭에서 처리된다.
2.2 Deep Learning Block
이 블럭의 목표는 거래할 통화 (해당 논문에서는 EUR/USD)에 대한 중단기 트랜드의 첫번째 예측을 결정하는 것이다. 이 블럭의 아키택처는 deep LSTM 신경망을 기반으로 한다. LSTM에 대한 확실한 설명은 [22, 23]에서 볼 수 있다. LSTM은 기본적으로 RNN(recurrent neural networks)의 특정한 타입이며 장기적인 것에 주목할만한 특징을 가진다. LSTM의 기본적인 유닛은 cell이다. 각 셀들은 input ,forget, ouput으로 이루어진 세개의 포트를 가지고 있으며 세개의 포트는 시그모이드 activation function으로 데이터를 처리한다. 이때 입력과 상태는 tanh activation function으로 변형된다. 셀은 이전의 게이트들이 입력, 임의적 시간 간격 동안 값을 기억한다. Figure 4는 셀 하나의 세부사항과 함께 LSTM의 고전적인 모델을 보여준다. Figure 5는 이번 논문에서 사용하는 LSTM 셀을 보여준다.


LSTM 셀 하나의 수학적 기호는 아래와 같다.
$ f_t = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f), $ (2)
$ i_t = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i), $ (3)
$ \tilde{C_t} = tanh(W_C \cdot [h_{t-1}, x_t] + b_C), $ (4)
$ C_t = f_t * C_{t-1} + i_t * \tilde{C_t}, $ (5)
$ o_t = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o), $ (6)
$ h_t = o_t * tanh(C_t), $ (7)
- $W_f, W_i, W_C, W_o$는 LSTM의 가중치를 나타낸다.
- $b_f, b_i, b_C, b_o$는 각 셀의 사용되는 bias를 나타낸다.
- $C_t$는 각 셀의 상태를 나타낸다.
그러므로, LSTM에서 데이터가 처리될 때 입력값은 위에서 정의된 식으로 처리되며 유지할 데이터와 잊을 데이터를 결정한다. 구체적인 LSTM의 아키텍처는 [24]에서 알 수 있다.
LSTM 아키텍처는 시그널 혹은 입력값에 있는 데이터를 효율적으로 분류하기 위해 사용할 수 있다[25, 26]. 이러한 이유로 저자는 단계적으로 제안한 딥 파이프라인 기반의 LSTM과 fully-connected 신경망과 소프트맥스 레이어 그리고 classifier을 사용한다. 마지막 분류 레이어는 각각의 입력값을 각각의 상호배타적 클래스로 할당하고 각 index의 오류와 수행을 계산하기 위해 소프트맥스 activiation 함수로 부터 계산된 결과가 사용된다. 이러한 방법을 우리의 파이프라인은 입력값을 LSTM 셀로 처리하여 소프트맥스 레이어와 분류자를 통해 적절히 feature를 분류한다. 비록 금융과 다른 분야이긴 하지만 비슷한 파이프라인이 효과적으로 사용되고 있다[27-31]. 이러한 점은 LSTM과 같은 입력값에서 특징을 추출하는 딥 네트워크를 소프트멕스 블럭과 연결하는 것이 식별하는 것에 잘 작동한다는 것을 보여준다. 제안된 된 아케틱처는 아래의 요소를 포함된다:
- Input Layer
- LSTM Layer (Hidden Cell Number)
- LSTM Layer (Hidden Cell Number)
- Fully Connected Layer (Number Classes)
- SoftMaxLayer
- Classification Layer
제안된 파이프라인에서 Hidden Cell Number는 각 LSTM 레이어의 셀의 개수이며 300개이다. Number Class는 class의 개수이며 3개이다. class에서 값 (0)은 단기 트랜드를 의미하며 (1)은 장기 트랜드를 (2)는 거래 구간에서 트랜드가 없음을 나타낸다. 트랜드가 없음은 다시말해 경제학 용어로 현재 상품에서 잘 정의된 트랜드가 없음을 나타낸다.
제안된 파이프라인에서 시계열 환율 입력값은 다음과 같은 방법으로 나뉜다. 명확한 길이의 부분으로 앞서 말한 딥 파이프라인의 입력값으로 사용되며 동인할 길이의 다음 시세의 환율 트랜드를 예측한다. 현재 케이스에서는 우리는 입력값과 결가값의 구간은 100 캔들스틱으로 한다. 이때 한 캔들스틱은 1분을 의미한다. 각 구간의 가격은 구간의 종가를 의미한다. 우리가 트랜드를 예측하는 것은 EUR/USD이며 우리가 사용할 삼각 차액거래 환율은 EUR/USD, EUR/GBP, GBP/USD이다. 따라서 각 100분의 종가를 데이터로 사용하여 다음 100분의 EUR/USD 종가를 예측한다. Figure 6은 앞서 말한 학습 과정을 보여준다.

LSTM으로 예측된 트랜드는 다음블록인 강화학습 정정 블럭의 입력값으로 들어간다.
2.3 RL Correction Block
이 블럭의 목표는 이전의 딥러닝 블럭으로 예측한 통화 가격을 정정하고 검증하는 것이다. 이전 블럭의 성능을 보여주는 테스트를 보면 그리 좋지 않다. 실제로 예를들어 2018년의 3개의 환율의 1분 구간을 주었을 때 이전블락의 정확도는 평균적으로 70% 정도이다. 이는 아래의 Figure 7에서 명확히 볼 수 있다.

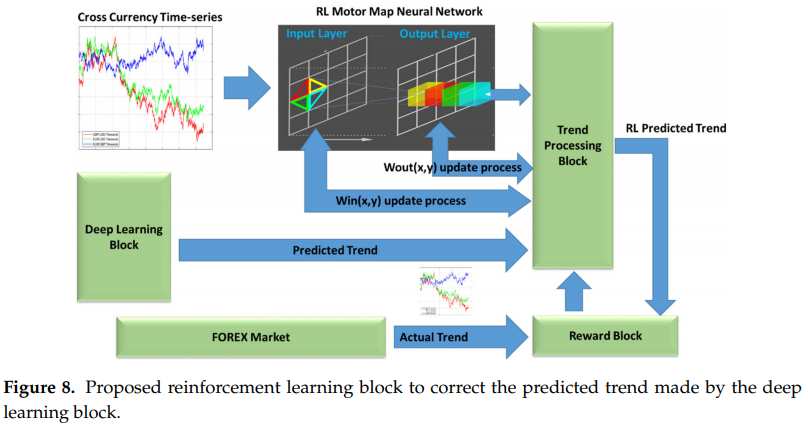
이러한 이유로 저자는 강화학습 기반의 비지도 딥러닝 정책을 사용하는 추가적인 학습 레이어 알고리즘을 적용하였다. 아래의 Figure 8은 이 블럭해서 구현된 파이프라인을 보여준다.
SOM(Self-Organizing Map)
SOM이란 사람이 눈으로 볼 수 있는 저차원 격자에 고차원 데이터의 각 개체들이 대응하도록 인공 신경망과 유사한 방식의 학습을 통해 군집을 도출해내는 기법.
각각의 입력백터들이 들어오면 각 노드들을 입력 벡터와 거리순으로 정렬해 가까운 순으로 입력벡터와 더 많이 가깝게 배치한다.
t시점의 j번째 격자벡터를 업데이트 하는 과정을 수식으로 나타내면 아래와 같다.
$$w_j^{t+1} = w_j^t + \mu_t\lambda_x^{j,t}[x - w_j^t]$$
아래의 그림은 학습의 진행을 보여준다.s

Figure 8에서 볼 수 있듯이, 전체적인 트랜드 예측 파이프라인의 성능을 증가시키기 위해 사용하는 강화학습의 가장 중요한 부분은 motor map architectur를 기반으로 한다. 이 아키텍쳐는 SOM network가 motor cortex의 방법으로 motor 뉴런을 흉내내서 주어진 actions에 대해 map 하는것이다. 즉 다시 말해 SOM network는 입력레이어의 SOM과 출력 레이어의 SOM이 나누어져 있으며 입력레이어의 결과값이 출력레이어의 입력 값으로 들어가 적절한 결과를 도출한다. Motor map 알고리즘의 경우 입력 레이어에서는 winner take all 방식으로 가장 가까운 노드와 그 이웃들만 값이 업데이트 된다. 반면 출력 레이어의 경우 무작위 주도 방법을 적용한다. 세부적인 내용과 적용은 [28, 32] 관련 논문에서 볼 수 있다.
Figure 8에서의 강화학습 알고리즘에 대해 진행하자. 우리는 $W^k_{in}(x, y)$와 $W_{out}(x, y)$을 각각 강화학습 Motor map에 사용하는 입력 가중치와 출력 가중치의 행렬이라고 정의한다. RL motor map은 30 X 30 격자 구조를 사용한다. 두 레이어 모두 무작위로 초기화한다. 입력 가중치의 경우 실질적 값을 추정하는 반면 출력 가중치 $W_{out}(x_k, y_k)$ short trend, long trend, trading arange 세개의 이산적인 값을 추정한다.
조금 정리를 하자면, 위의 그림에서 검은색 점들이 traing set이며 해당 검은색 점들을 하나씩 넣어가며 가장 가까운 격자 벡터를 찾아 자신에 가깝게 만든다. 이를 모든 트레이닝 셋을 통해 학습시켜 격자 벡터를 군집화 시킨다. 이때 가까운 격자 벡터는 더 많이 가까워지며 멀리있는 격자벡터는 거의 가까워 지지 않는다. 격자 벡터를 모두 학습시키면 이제 입력 레이어가 완성되었다. 입력 레이어는 입력값을 넣으면 넣으면 해당 입력값에 가장 가까운 격자의 x, y좌표를 출력한다. 이를 출력 레이어의 입력값에 넣어 이전과 같이 SOM Network를 사용하여 세가지 트랜드를 반환한다.
앞서 말한 세개의 환율을 정규화 해서 RL Motor map의 입력값으로 넣는다. 입력 레이어의 각 뉴런에서 뉴런과 시계열 환율 정보에 대한 거리 $d(x, y)$가 결정된다. 따라서 환율의 값과 30 X 30개의 뉴런의 값의 거리를 나타내는 행열이 계산된다.

(8)의 식을 통해 계산한 행렬을 통해 유클리드 거리가 가장 가까운 뉴런(노드)을 선택한다. 우리는 가장 가까운 뉴런의 좌표를 $(x_{min}, y_{min})$이라고 부르겠다.
이제 출력 레이어에서 $(x_{min}, y_{min})$에 해당하는 위치를 생각하자. 이것은 우리가 예측하려고 하는 환율의 트랜드에 해당하는 결과 $w_{out}(x_{min}, y_{min})$의 가중치 값을 만들 것이다. 이것을 식으로 작성하면 아래와 같다.

환율 트랜드를 올바르게 예측하기 위한 최적화된 정책 $P_t$을 결정하기 위해 강화학습은 체계이 상태를 나타내는 $s_t$를 고려할 것이다. 이때 체계는 아와 같은 것을 포함한다.
$$system = x^t_{min}, y^t_{min}, d^t(x^t_{min}, y^t_{min}), w^t_{out}(x^t_{min}, y^t_{min}), p_c^{EUR/USD}(t_k), p_c^{EUR/GBP}(t_k), p_c^{GBP/USD}(t_k), N, trend_{p-Deep Learning}$$
우리는 따라서 상태 $s_t$에 해당하는 학습 step 't'를 나타내기 위해서 각 변수의 첨자로 추가했다. 또한 $tread_{p-Deep Learning}$을 이전의 딥러닝 블럭에서 예측된 결과로 정의했다. 수학적 식으로 문제를 정의해 아래와 같이 나타내었다. 우리는 action $a_t$을 다음 100개 구간에서 가장 그럴듯한 EUR/USD 환율의 중기 트랜드로 정의했다. 우리는 agent를 정의하고 action $a_t$를 선택했다. 우리는 누적 할인 보상을 최소화하는 최적화된 정책 $P_o$을 찾기 위해 노력했다.

여기서 $\gamma$는 (0, 1)에서의 적절한 할인율을 의미한다. 보상 함수 $R(.)$은 아래와 같다. 여기서 식에서는 잘못 나타나 있다. 아래의 min 두개는 모두 max로 보아야 한다.

여기서 $E^t_{Deep-Learning}, E^t_{w^t_{out}(x^t_{min}, y^t_{min})}$은 각각 이전의 딥러닝 블럭에서 예측된 트랜드의 오류와 강화학습 motor map의 결과 $w^t_{out}(x^t_{min}, y^t_{min})$의 오류로 아래와 같이 결정된다.

정책 $P_o$는 따라서 각 스탭마다 딥러닝 블럭에서 추측한 값과 Motor map에서 추측한 값 $w^t_{out}(x^t_{min}, y^t_{min})을 검증하여 보상을 최소화 하는 예측을 결정하거나 혹은 무작위 업데이트를 진행해서 새로운 예측을 결정해야 한다. 구체적을 말하면 agent는 아래의 식과 같이 행동한다. 여기서 min은 모두 max로 보아야 한다.

만약 딥러닝 블럭의 예측값과 Motor map의 예측값이 모두 틀리면 아래와 같이 $w^t_{out}(x^t_{min}, y^t_{min})$을 업데이트 한다.

이 단계가 결정되었다면 우리는 입력 레이어의 가중치를 RL motor map이 맞을때만 업데이트를 한다. 해당 경우는 아래의 경우와 같다. 아래의 경우도 마찬가지로 min이 아니라 max로 수정해야 한다.

(16)의 식이 맞다면 입력레이어의 가장 가까운 뉴런 즉, $(x^t_{min}, y^t_{min})$의 좌표에 있는 뉴런을 입력으로 들어운 시계열 환율에 가깝게 이동한다. 이러한 방법으로 이전의 딥러닝 블럭에서 도출된 예측값을 적절히 수정하면서 입력값에 특정한 패턴을 찾도록 RL motor map을 학습시킨다. 입력 가중치는 아래의 식과 같이 업데이트 된다.

여기서 $\beta$는 학습율을 의미하고 ($\beta = 0.15$로 정의), $\varphi(p^\xi_c(k))$는 시계열 환율 정보에서 한 구간의 종가를 의미한다. $\sigma(x^t_{min}, y^t_{min})$는 일반적인 adaptive 가우시안을 사용하여 가장 가까운 뉴런의 이웃 뉴런들을 업데이트하는 function을 의미한다[25, 29]. 아래의 Figure 9는 RL motor map을 학습하면서 줄어드는 보상 함수를 볼 수 있다.

RL 프레임워크로 딥러닝 블럭을 정정하는 시스템의 경우 전체적인 평균 정확도를 향상시켜 85% 가량으로 만들어 주었으며 robustness와 effectiveness를 가져다 주었다. 테이블 1은 Figure 8의 파이프 라인의 RL 트랜드 정정 블럭이 있을 때와 없을 때의 검증 결과를 보여준다.

정확도의 측면에서 딥러닝 블럭만 있는 모델은 RL 파이프 라인이 있는 모델보다 떨어지는 것을 알 수 있다. 이것은 다양한 년도에서 EUR/USD 환율로 시험을 해봤을때 분명하였다.
2.4. Currency Trend Forecast Application: HFT Grid Trading System
이전 섹션에서 딥러닝과 강화학습을 사용하여 삼각 차액거리라고 불리는 금융 테크닉을 사용하여 환율을 분석하여 환율의 중단기 트랜드를 분석하는 예측 파이프 라인을 설명하였다. 이제 중기 트랜트의 예측을 할 수 있으므로 이제는 예측을 바탕으로 연속적인 매매를 할 수 있는 거래 전략을 계획하는 것이 필요하다. 이것을 적용하기 위해 저자는 [2]에서 잘 묘사되어 있는 gird를 통한 HDT 알고리즘을 사용하려 한다.
기본적으로, 그리드 트레이딩은 적절한 기준 가격에서 어느정도 위 아래오 가격 구간을 두어 매도와 매수를 걸어서 시장의 변동에 이익을 얻는 것이다. 우리의 경우 아래와 같이 거래가 작동한다.
이전 섹션에서 말한 방법으로 예측 시스템을 사용하여 중기 트랜드가 생성된다. 예측된 트랜드를 기반으로 long trend에는 매수를 short trend에는 매도를 건다. [2]에서 설명되어 있는 조정하는 grid methodology를 사용하여 전체적인 drawdown이 늘어나면 매도 혹은 매수 사이의 가격 구간을 넓게 띄우고 반대로 drawdown이 낮아지면 가깝게 한다. 만약 파이프라인이 trading ragne 예측을 냈다면 거래 시스탬은 어떠한 거래도 하지않고 홀드한다. 이전에 말했듯이 우리는 EUR/USD 환율에 이것을 적용하였다. 다름 문단에서는 확실하게 제안한 방법을 통해 시험한 결과를 보여줄 것이다.
Drawdown : 자본의 최고점과 최저점의 차이이다. 내려간 금액 만큼 다시 되찾으려면 더 많은 %가 올라야 하므로 안정성을 평가하는데 중요한 척도가 된다.
3. Discussion and Conclusions
우리는 완전하고 종합적인 데이터를 사용하여 우리의 파이프라인을 정확히 평가하였다. 이것의 ad-hoc financail 데이터 셋을 제대로 준비하였다. 환율 데이터 셋의 겨웅 99%의 정확도를 가지고 1분 간격의 단위로 2004-2018 기간의EUR/USD, GBP/USD, EUR/GBP 환율을 Tickstory website[33]에서 다운로드 하였다. 이전에 말한대로 70%가량의 데이터는 학습을 위해 30%는 validation와 test를 위해 사용하였다. 시뮬레이션은 AMD Ryzen 16 Cores와 쿠다를 지원하는 Nvidia RTX 2080 Ti GPU 를 가진 서버와 MATLAB 2018b fulltoolboxes를 사용하였다. 우리는 초기 자본으로 30000$를 가진 계좌를 가정하였고 bid/ask spread를 2 pip으로 가정하였다. 우리는 계좌 레버리지를 1:400으로 가정했고 각각의 거래마다 LOT size로 체결하였다[2].
- pip이란 point in percentage의 약자로 외환시장에서 두 통화 사이에서의 가치의 가장 작은 변화를 정의하는데 사용하는 측정단위이다. 일반적으로 소수점 넷째자리가 기준이 된다.
- 외환시장에서는 매수가를 bid 매도가를 ask라고 하며 이 bid와 ask의 차이를 spread라고 한다.
- LOT이란 제품 혹은 서비스의 그룹을 말하며 외환시장에서는 통화의 standard set을 말한다. LOT에는 Stndard Lot, Mini Lot등 다양한 LOT이 있지만 일반적으로 Standard Lot을 말하며 이는 외환 시장에서 100,000 unit을 말한다. 이는 미화로 따지면 10$와 같다.
외환 거래 시스템과 유사하게 비교기준을 설정하기 위해 아래의 index를 정의 하였다.
$$ROI = \frac{100 * (Gain - Investment)}{Investment} (18)$$
$$MD = \frac{\left | BalanceValley - BalancePeak \right |}{BalancePeak} (19)$$
제안된 방법은 가능한 모든 2004년부터 2018년 까지 가능한 모든 해에 다른 날의 time-window에서 검증하였다. 테이블2는 제안된 방법과 비슷한 다른 방법과 비교하였다. (모든 방법은 같은 환율과 같은 사이트의 데이터 셋을 비교하였다.)
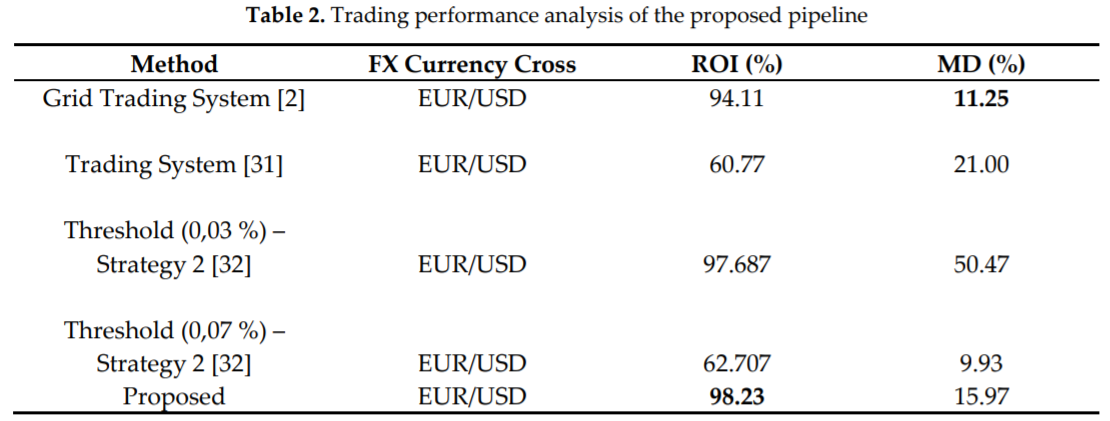
고빈도 트레이딩에 대해서 제안된 방법은 [2]에서 제안된 방법에 비해 훨씬 많은 연산량을 가진다. 좋은 트랜드 예측 성능을 통해 증가된 거래량은 제안된 고빈도 시스탬이 수익성이 있으며 적절한 drawdown이 있음을 의미한다. 이는 시간단위가 1분단위여서 어느정도 환율의 변동성이 제한된 이유도 있다. 제안된 방법의 경우 예측된 트랜드가 좋을 경우 하루에 50번에서 100번 정도의 외환거래가 이루어지므로 고빈도 시스템에 들어간다. ROI 지표는 Maximum Drawdown(MD)와 함께 보았을 때 큰 중요성을 가진다.

테이블 3에서 볼 수 있듯이 ROI는 거의 상수와 같으나 MD 값의 경우 다양함을 알 수 있다. MD 값의 경우 평균 15.97% 였으며 더 나은 MD가 연구되어야 함을 알 수 있다. Figure 10은 제안된 시스템의 GUI instance를 보여준다.

테이블 2에서 보면 [2]에서 제안한 모델보다 ROI는 좋으나 MD가 더 큼을 알 수 있는데 이는 정해진 기간을 예측하는 것이 아닌 중기 트랜드를 예측함을 통해 거래를 하는 이유때문이다. 이는 평균적인 MD의 증가를 불러일으켰지만 더 넓은 범위의 금융 가격 예측을 할 수 있다.
References
1. Rundo, F.; Trenta, F.; Di Stallo, A.L.; Battiato, S. Advanced Markov-Based Machine Learning Framework for Making Adaptive Trading System. Computation 2019, 7, 4.
2. Rundo, F.; Trenta, F.; di Stallo, A.L.; Battiato, S. Grid Trading System Robot (GTSbot): A Novel Mathematical Algorithm for Trading FX Market. Appl. Sci. 2019, 9, 1796.
3. Nti, I.K.; Adekoya, A.F.; Weyori, B.A. A systematic review of fundamental and technical analysis of stock market predictions. Artif. Intell. Rev. 2019, 1–5, doi:10.1007/s10462-019-09754-z.
4. Vlasenko, A.; Vlasenko, N.; Vynokurova, O.; Bodyanskiy, Y.; Peleshko, D. A Novel Ensemble Neuro-Fuzzy Model for Financial Time Series Forecasting. Data 2019, 4, 126.
5. García, F.; Guijarro, F.; Oliver, J.; Tamošiūnienė, R. Hybrid fuzzy neural network to predict price direction in the German DAX-30 index. Technol. Econ. Dev. Econ. 2018, 24, 2161–2178, doi:10.3846/tede.2018.6394.
6. Li, Y.; Zheng, W.; Zheng, Z. Deep Robust Reinforcement Learning for Practical Algorithmic Trading. IEEE Access 2019, 7, 108014–108022.
7. Si, W.; Li, J.; Ding, P.; Rao, R. A Multi-objective Deep Reinforcement Learning Approach for Stock Index Future’s Intraday Trading. In Proceedings of the 2017 10th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 9-10 December2017; pp. 431–436.
8. Chen, T.; Su, W. Local Energy Trading Behavior Modeling With Deep Reinforcement Learning. IEEE Access 2018, 6, 62806–62814.
9. Kumar, P.H.; Patil, S.B. Forecasting volatility trend of INR USD currency pair with deep learning LSTM techniques. In Proceedings of the 3rd International Conference on Computational Systems and Information Technology for Sustainable Solutions (CSITSS), Bengaluru, India, 20-22 December2018; pp. 91–97.
10. Ma, Y.; Han, R. Research on stock trading strategy based on deep neural network. In Proceedings of the 18th International Conference on Control, Automation and Systems (ICCAS), PyeongChang , Korea, 17–20 October 2018; pp. 92–96
11. Chen, C.T.; Chen, A.; Huang, S. Cloning Strategies from Trading Records using Agent-based Reinforcement Learning Algorithm. In Proceedings of the IEEE International Conference on Agents (ICA), Singapore, 28–31 July 2018; pp. 34–37.
12. Korczak, J.; Hemes, M. Deep learning for financial time series forecasting in A-Trader system. In Proceedings of the Federated Conference on Computer Science and Information Systems (FedCSIS), Prague, 3–6 September 2017; pp. 905–912.
13. Wang, J.; Sun, T.; Liu, B.; Cao, Y.; Wang, D. Financial Markets Prediction with Deep Learning. In Proceedings of the 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, 17–20 December 2018; pp. 97–104.
14. Lee, R.S.T. Chaotic Type-2 Transient-Fuzzy Deep Neuro-Oscillatory Network (CT2TFDNN) for Worldwide Financial Prediction. IEEE Trans. Fuzzy Syst. May 2019, doi:10.1109/TFUZZ.2019.2914642.
15. Zarkias, K.S.; Passalis, N.; Tsantekidis, A.; Tefas, A. Deep Reinforcement Learning for Financial Trading Using Price Trailing. In Proceedings of the ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 3067–3071.
16. Shleifer, A.; Vishny, R. The limits of arbitrage. J. Financ. 1997, 52, 35–55, doi:10.1111/j.1540- 6261.1997.tb03807.
17. Conoci, S.; Rundo, F.; Petralta, S.; Battiato, S. Advanced skin lesion discrimination pipeline for early melanoma cancer diagnosis towards PoC devices. In Proceedings of the IEEE 2017 European Conference on Circuit Theory and Design (ECCTD), Catania, Italy, 4–6 September 2018;
18. Rundo, F.; Conoci, S.; Banna, G.L.; Stanco, F.; Battiato, S. Bio-Inspired Feed-Forward System for Skin Lesion Analysis, Screening and Follow-Up. In Image Analysis and Processing - ICIAP 2017. ICIAP 2017. Lecture Notes in Computer Science, vol 10485. Springer, Cham, pp. 399–409.
19. Rundo, F.; Conoci, S.; Banna, G.L.; Ortis, A.; Stanco, F.; Battiato, S. Evaluation of Levenberg–Marquardt neural networks and stacked autoencoders clustering for skin lesion analysis, screening and follow-up. IET Comput. Vis. 2018, 12, 957–962.
20. Ortis, A.; Rundo, F.; Di Giore, G.; Battiato, S. Adaptive Compression of Stereoscopic Images. In Image Analysis and Processing – ICIAP 2013. ICIAP 2013. Lecture Notes in Computer Science, vol 8156. Springer, Berlin, Heidelberg pp 391-399.
21. Banna, G.L.; Camerini, A.; Bronte, G.; Anile, G.; Addeo, A.; Rundo, F.; Zanghi, G.; Lal, R.; Libra, M. Oral metronomic vinorelbine in advanced non-small cell lung cancer patients unfit for chemotherapy. Anticancer Res. 2018, 38, 3689–3697.
22. Gers, F.; Schmidhuber, E. LSTM recurrent networks learn simple context-free and context-sensitive languages. IEEE Trans. Neural Netw. 2001, 12, 1333–1340, doi:10.1109/72.963769.
23. Gers, F.; Schraudolph, N.; Schmidhuber, J. Learning precise timing with LSTM recurrent networks. J. Mach. Learn. Res. 2002, 3, 115–143.
24. Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780.
25. Jithesh, V.; Sagayaraj, M.J.; Srinivasa, K.G. LSTM recurrent neural networks for high resolution range profile based radar target classification. In Proceedings of the 3rd International Conference on Computational Intelligence & Communication Technology (CICT), Ghaziabad, India, 9–10 February 2017; pp. 1–6.
26. Balouji, E.; Gu, I.Y.H.; Bollen, M.H.J.; Bagheri, A.; Nazari, M. A LSTM-based deep learning method with application to voltage dip classification. In Proceedings of the 18th International Conference on Harmonics and Quality of Power (ICHQP), Ljubljana, Slovenia, 13–16 May 2018; pp. 1–5.
27. Rundo, F.; Petralia, S.; Fallica, G.; Conoci, S. A nonlinear pattern recognition pipeline for PPG/ECG medical assessments. In CNS Sensors, Lecture Notes in Electrical Engineering; Springer: Cham, Switzerland, 2018; Volume 539, pp. 473–480.
28. Rundo, F.; Ortis, A.; Battiato, S.; Conoci, S. Advanced Bio-Inspired System for Noninvasive Cuff-Less Blood Pressure Estimation from Physiological Signal Analysis. Computation 2018, 6, 46.
29. Mazzillo, M.; Maddiona, L.; Rundo, F.; Sciuto, A.; Libertino, S.; Lombardo, S.; Fallica, G. Characterization of sipms with nir long-pass interferential and plastic filters. IEEE Photon. J. 2018, 10, 1–12.
30. Vinciguerra, V.; Ambra, E.; Maddiona, L.; Romeo, M.; Mazzillo, M.; Rundo, F.; Fallica, G.; Di Pompeo, F.; Chiarelli, A.M.; Zappasodi, F.; et al. PPG/ECG multisite combo system based on SiPM technology. In CNS Sensors, Lecture Notes in Electrical Engineering; Springer: Cham, Switzerland, 2018; Volume 539, pp. 353- 360.
31. Rundo, F.; Banna, G.L.; Conoci, S. Bio-Inspired Deep-CNN Pipeline for Skin Cancer Early Diagnosis. Computation 2019, 7, 44.
32. Battiato, S.; Rundo, F.; Stanco, F. Self Organizing Motor Maps for Color-Mapped Image Re-Indexing. IEEE Trans. Image Process. 2007, 16, 2905–2915.
33. Tickstory—Historical Data & Resources for Traders. Available online: https://tickstory.com/ (accessed on 12 September 2019).
34. STM32 Platform. Available online: https://www.st.com/content/st_com/en/about/innovation--- technology/artificial-intelligence.html (accessed on 12 September 2019).
